HTTPS 的密码学基础
12月 2, 2021
本来打算直接总结下 HTTPS,但是发现要写的很多内容其实都依靠密码学的基础概念,其实我在阅读别的资料的时候发现基本也是这样,不然说的时候上下文都串不起来,甚至可以说研究 HTTPS 约等于在研究加密算法。所以还是专门分一篇来说一下加密,这样后面说 SSL/TLS 的时候就可以拉通底层概念了。
对称加密算法 #
对称加密算法(Symmetric-Key Algorithm)的详细内容可以直接参考我之前的文章:AES 对称加密学习笔记。
简单来说,对称加密的要素为:明文、密钥和密文,通过一个密钥就可以实现加密解密。对称加密解决了人们最基本的安全地加密解密的需求,但是如何给通信的双方同步密钥又是一个问题,这种问题也叫做密钥配送问题(Key Distribution Problem)。
密钥配送问题 #
假设通信的双方Alice 和 Bob 之间有一个做坏事的中间人 Mallory,由于通信所基于的 IP 协议是透明的,数据不会进行加密,中间人就可以通过各种手段截获并修改信息,中间人的这波破坏性操作一般叫做中间人攻击。
由于中间人 Mallory 的存在,Alice 用于加密的密钥是没有办法通过网络的方式安全地给到 Bob 的,为了解决这个问题,密码学家发明了公钥密码算法。
公开密钥算法 #
相对于对称加密,公开密钥算法(Public-Key Cryptography )也叫做非对称加密算法(Asymmetric Cryptography)。与对称加密的密钥的区别是,公开密钥算法里有两个密钥,一个叫做公钥,一个叫做私钥。其中私钥用来加密,公钥用来解密,这样公钥就可以在网络里传播,但只用来解密数据,私钥一般保存在本地(或服务器)只用来加密,如此一来就避免了中间人篡改消息的攻击。
常见的公开密钥算法有 RSA 算法、Diffie-Hellman 密钥交换协议中的公钥加密算法,先介绍下最常见的 RSA。
RSA 算法原理 #
在 RSA 算法中,加密解密的公式如下:
$$ 密文 = 明文^E \mod N $$
$$ 明文 = 密文^D \mod N $$
其中:
- 可见私钥由 $D$ 和 $N$ 组成,公钥由 $E$ 和 $N$ 组成。
- $N$ 通常为两个很大的质数 ($p$, $q$) 的乘积,如 $N = p \times q$。
- 设一个 $L$,$L$ 为 $p-1$ 和 $q-1$ 的最大公倍数,$L = (p-1) \times (q-1)$。
- $E$ 为比 $L$ 小同时大于 $1$ 数,同时 $E$ 和 $L$ 的最大公约数必须为 $1$。
- $D$ 也为比 $L$ 小同时大于 $1$ 的数,同时满足:$E \times D \mod L = 1$
可见如果要破解的话,基本是通过$密文$、$E$ 和 $N$ 求 $D$ 和$明文$,就是一个幂运算+模运算的逆向求解,即为离散对数求解,这在数学上是非常困难的,暴力破解的难度随着 $D$ 的长度增加而增加。通常来说,一个 2048bit 的密钥就被认为是安全的。
对 RSA 的攻击 #
(1)中间人攻击
在这种场景下,中间人攻击虽然不能篡改 Alice 发给 Bob 的密文,但是可以拦截密文,通过重新生成一份密文和公钥发给 Bob,Bob 也会透露机密信息然后用 Mallory 的公钥加密发给 Alice,Mallory 只要再次拦截 Bob 的消息进行修改就可以让 Alice 误以为是 Bob 的回复。
(2)选择密文攻击
网络上有很多服务在收到错误的请求时都会报错,攻击者可以根据不同的错误提示(可以说是解密提示)来获得关键信息,进而发起攻击。
算法特点 #
- 于是底层的实现原理的复杂性,公钥密码算法的计算一般都比较慢。
- 适合与其他算法一起使用,比如大量数据使用对称加密,少量数据使用非对称加密,后面还会介绍。
- 可以解决密钥配送问题,但单独使用还是存在一定的安全问题,可以配合后面讲的证书一起使用。
单向散列函数 #
有的时候,我们不需要对信息进行加密,只是想确认信息(或文件)的完整性,或者说防止有人篡改过数据,这时就需要单向散列函数了,也叫单向哈希函数,它是一种消息摘要算法。顾名思义,就是单向加密,无法反向破解,生成的散列值可以理解为是一段数据的“指纹”。
单向散列函数具有如下特点:
- 任意长度的消息可以计算出固定长度的散列值。
- 计算速度很快。
- 任意不同的消息,散列值也不同。
- 不需要密钥。
在衡量安全性方面,主要是考虑算法的抗碰撞性,即:
- 弱抗碰撞性:找到和该消息具有相同散列值的另外一条消息。
- 强抗碰撞性:找到两条散列值相同的不同消息。
MD5 #
MD5 由于强抗碰撞性被攻破已不推荐。
SHA #
SHA1 和 SHA2 都已被攻破。
SHA3 特点:
- 输入长度没有限制。
- 基于双工结构的 Keccak 算法,即在输入数据的同时可以输出。
- 根据散列值长度可以分为 SHA3-224、SHA3-256、SHA3-384、SHA3-512 四个版本。
以 SHA3-256 为例,对于任意长度的消息,SHA3-256 都会产生一个 256 位的哈希值,称作消息摘要。这个摘要相当于是个长度为 32 个字节的数组,通常有一个长度为 64 的十六进制字符串来表示,其中 1 个字节等于 8 位,一个十六进制的字符的长度为 4 位。
加盐 #
单纯地只使用单向散列函数有一个很大的弊端,就是明文对应的哈希值永远是一样的,很容易被坏人利用进行字典攻击,所以有时我们可以通过伪随机数生成算法来生成一个随机串,称之为加盐,然后再把盐值与明文合起来进行散列值计算,就可以得到一个破解复杂度陡增的散列值了。
消息认证码 #
消息认证码(Message Authentication Code)简称 MAC,是一种确认完整性并进行认证的技术。消息认证码和单向散列函数的区别就是使用消息认证码的场景里需要密钥,这个密钥可以是对称加密的密钥,也可以公钥算法的密钥,不过使用起来会有差别。
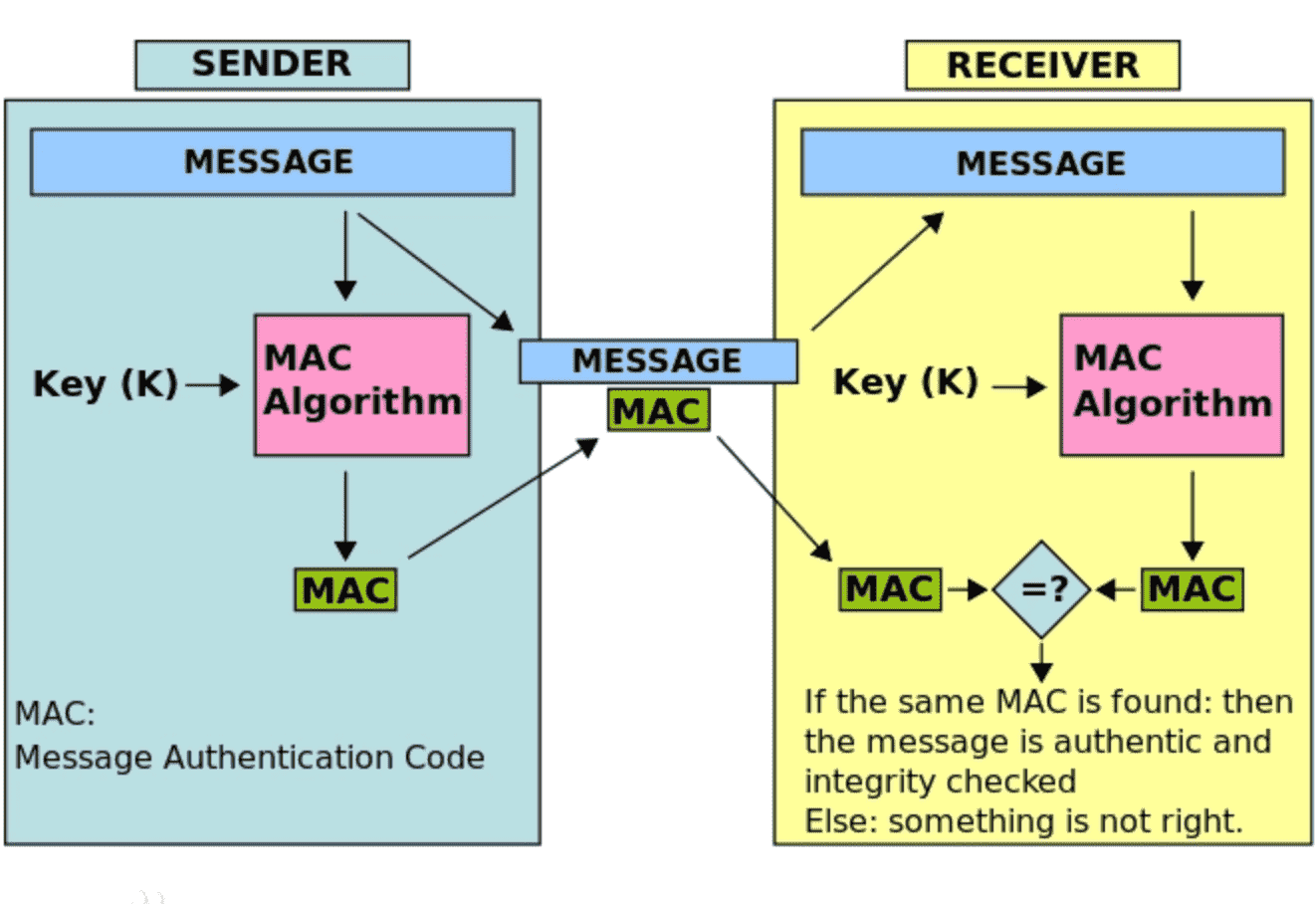
在上图中,消息的发送方通过 MAC 算法生成结果 v1,然后将消息和 v1 一起发送给接收方。接收方使用相同的 MAC 算法得到消息的 MAC 值 v2,通过 v1 和 v2 进行比较可以判断消息在传输期间是否保持数据完整。是不是有签名那味儿了?
HMAC 实现 #
这里的 H 就是 hash 的意思,是一种使用单向散列函数来构造消息认证码的方式,具体算法也就是 HMAC-SHA-224、HMAC-SHA-256、HMAC-SHA-384、HMAC-SHA-512 等那几种。
存在的问题 #
再回到上面提到的一个中间人攻击的问题,MAC 只是验证了消息确实是发送人发送的完整数据,但是并不能验证 Alice 就是发送人,中间人 Mallory 也可以篡改消息重新作为发送人自己对新的消息进行 MAC 认证,Alice 也可以借助这个原因抵赖之前发过的消息,于是我们终究还是要引入签名的概念。
数字签名 #
签名理解起来就是需要 Alice 在发送消息的时候,用自己的笔迹对消息进行签名,这样 Bob 看到是 Alice 的笔迹就可以确信消息确实是发自 Alice,没有被篡改过。
签名者使用公开密钥签名算法和对应的私钥签署消息得到签名值,然后将签名值和原始消息发送给接收者。接受者收到签名值和原始消息后,使用签名者的公钥验证签名,一旦验证通过,代表该条消息确实是公钥主人(签名者)签发的,而且签名者不能抵赖。
请注意,只有拥有私钥的人才能对信息进行签名,但是有公钥的所有人都可以验证它,即:
发送人 Alice 的生成签名 -> 私钥加密生成
接收人 Bob 的验证签名 -> 公钥解密验证
这个过程和公开密钥算法好像正好相反:
发送人 Alice 使用公钥加密数据
接收人 Bob 使用私钥解密数据
数字签名实际用到的其实也是公开密钥算法。由 RSA 里介绍的公式可得,用公钥加密所得的密文,只能用相配对的私钥才能解密,同样的,用私钥加密所得的密文,也只能用相配对的公钥才能解密,如下公式:
$$ 签名 = 消息^D mod N $$
$$ 消息 = 签名^E mod N $$
这里的私钥还是由 D、N 组成,公钥还是由 E、N 组成,和上面的公开密钥算法一致。对比下公式可以发现,加密解密的概念只是相对这两种场景来说正好相反,但是不变的是公钥计算(EN)和私钥计算(DN),公式本身没有变,变得是计算对象的值而已。换句话说,进行公钥计算的对象,再进行一次私钥计算,就是自己本身。
通过 RSA 实现 #
还是假设 Alice 给 Bob 发送消息:
- 由于消息一般比较大,公开密钥算法有比较费时,在实际应用中,一般会将消息现进行散列计算,再用 Alice 自己的私钥对散列值进行 RSA 加密得到签名。最后将消息和签名一起发送,消息可以通过 AES 对称加密算法进行加密。
- Bob 收到消息和签名后,用 Alice 的公钥进行签名进行解密得到散列值,如果得到的散列值和消息的散列值一致,说明签名验证成功。
我们也可以发现,数字签名技术已经是上述所有算法的综合应用了。另外除了 RSA 也有一些其他的数字签名技术,比如 DSA 数字签名算法。
通过 DSA 实现 #
DSA 算法是数字签名技术标准(DSS)的标准算法,它只能进行签名,不能进行加密解密。DSA 算法需要三个公共参数:p、q、g,并由此生成私钥和公钥。
还有安全问题吗 #
虽然数字签名解决了 抵赖(Alice)、篡改(Mallory) 的问题,但是还是有一个问题,Bob 手里的公钥,如何知道就是 Alice 的呢?即如何保证接收者的公钥属于真正的发送者?要彻底解决中间人攻击的问题,我们最后还需要引入证书的概念。
证书 #
证书就是一个权威的证书颁发机构(简称 CA,Certificate Authority)对一个证书申请人的认证。认证后,会对申请人的公钥进行签名,并把公钥放到数字证书上。进行 HTTPS 通信时,服务器会把证书发送给客户端,客户端取得其中的公开密钥之后,先进行验证,如果验证通过,就可以开始通信。
证书的结构 #
通过浏览器地址栏左侧的绿锁标志,可以点进去查看证书详情,下图为 google.com 的例子。

这里重点介绍几个字段。
版本号:证书一共有 3 个版本号,分别用 0、1、2 编码表示版本 1、版本 2 和版本 3。版本 1 只支持简单的字段,版本 2 增加了两个标识符(新增的字段),而版本 3 则增加了扩展功能。现在大部分的证书都采用版本 3 的格式。
序列号:在一开始,序列号只要是正整数即可,是每个 CA 用来唯一标识其所签发的证书。但是在出现了针对证书签名的预选前缀攻击之后,序列号增加了更多的要求来防止此类攻击;现在序列号需要是无序的(无法被预测)而且至少包括20位的熵。
签名算法:这个字段指明证书签名所用的算法,需要放到证书里面,这样才能被证书签名保护。
颁发者(issuer):一般包括了证书颁发者的国家、组织和组织单位三个部分。
有效期:证书的有效期包括开始日期和结束日期,在这段时期内证书是有效的。
使用者(subject):是实体的可分辨名称,和公钥一起用于证书的签发,在自签名证书里,使用者和颁发者的内容是一样的。
公钥:就是证书使用者的公钥。
证书拓展:原本证书(1、2 版)的格式过于死板,版本 3 引入了证书扩展,每一个扩展包含唯一的对象标识符。
证书链 #
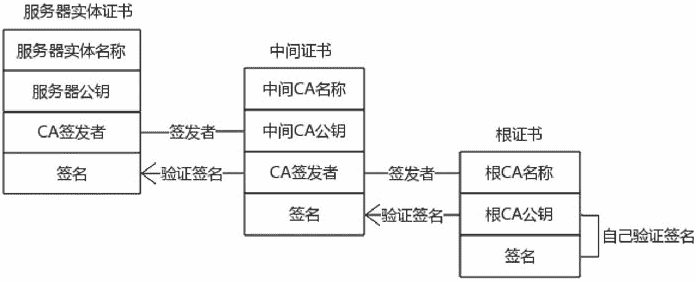
证书链构成了信任基础,是证书里最重要的概念。从证书链的角度看,证书可以分为三种类型,分别是服务器实体证书、中间证书、根证书。
根证书的样子参考上图,颁发机构是 GTS Root R1 自己,即根证书是自签名证书。
中间证书如下图:
实体证书如下图:

在证书链校验过程中,浏览器会发送完整的证书链给浏览器,浏览器从实体证书的上一级证书的公钥开始校验实体证书的签名,如果校验成功,则不断迭代校验证书的签发者的证书,直到发现某张证书的签发者和使用者是同一个人,代表找到了根证书。验证跟证书的公钥就在根证书中,如果校验成功这说明整个证书链校验成功。浏览器集成了各个 CA 机构的根证书,这是整个信任链的基础。
根据这个原理,我们自己也可以在本地生成自签名的根证书,可以用于 Charles 抓包获取 HTTPS 的加密信息。
证书吊销 #
除了证书链的验证,还有一些其他的验证,比如要验证证书的有效期和证书是否被 CA 机构吊销。
由于某些原因想让未过期的证书失效,就需要进行永久吊销或临时吊销。浏览器根据 CRL(Certificate Revocation List,证书吊销列表)进行证书吊销验证。
其他 HTTPS 相关算法 #
这里再介绍一些 HTTPS 场景中需要用到的算法。
密钥协商算法 #
常见的密钥协商算法有:RSA 公开密钥算法,Diffie-Hellman 密钥协商算法,密钥协商算法通常用来解决密钥分配、存储、传输等问题。
RSA 的公钥密钥算法,可以作为协商算法使用:
- 客户端初始化连接服务端,服务端发送 RSA 算法的公钥给客户端;
- 客户端生成一个随机数,这个值被称为会话密钥;
- 客户端使用服务端给的公钥加密这个“会话密钥”,然后发给服务端;
- 至此服务端和客户端都得到了要来做数据对称加密的会话密钥。
严格来说 RSA 公开密钥不算是密钥协商算法,因为密钥的生成完全由客户端控制,而 Diffie-Hellman 算法实现了真正的密钥协商,通信双方的任何一方无法独自计算出一个会话密钥,双方各自保留一部分关键信息,再将另外一部分信息告诉对方,双方有了全部信息才能共同计算出相同的会话密钥。
椭圆曲线加密算法 #
椭圆曲线加密算法(Elliptic Curve Cryptography,ECC)是新一代的公开密钥算法,主要的优点就是安全性,极短的密钥能够提供很大的安全性,ECC 算法的优势就是性能和安全性非常高。ECC 可以结合其他公开密钥算法形成更快、更安全的公开密钥算法,比如结合 DH 密钥协商算法组成 ECDH 密钥协商算法,结合数字签名 DSA 算法组成 ECDSA 数字签名算法。
随机数算法 #
通过计算机的算法只能实现伪随机数生成器,如果要实现真正的随机数算法必须依赖物理硬件。
名词解释 #
公钥基础设施 PKI (Public-Key Infrastructure),PKI 是一个总称,并非指某一个单独的规范或规格。RSA 公司制定的 PKCS (Public-Key Cryptography Standards,公钥密码标准) 系列规范是 PKI 的一种,互联网规格 RFC(Request for Comments) 也是 PKI 的一种,X.509 也是 PKI 的一种。每个公司编写的 API (Application Programming Interface,应用程序编程接口) 和规格设计书都可以算是 PKI 的相关规格。
X.509 是密码学里公钥证书的格式标准。X.509 证书已应用在包括 TLS/SSL 在内的众多网络协议里,同时它也用在很多非在线应用场景里,比如电子签名服务。X.509 证书里含有公钥、身份信息(比如网络主机名,组织的名称或个体名称等)和签名信息(可以是证书签发机构CA的签名,也可以是自签名)。
证书格式一般有 PEM、DER、CER 等。
参考 #
- 图解密码技术
- 深入浅出 HTTPS
- HTTPS 权威指南
- HTTPS 温故知新 | halfrost