常见的垃圾回收算法 Recommended

2月 28, 2021

本来想直接看下 Go 的垃圾回收机制，但是发现自己现在对内存管理和垃圾回收的了解都比较少，所以只能先来研究下常见的垃圾回收算法了，本篇即是《垃圾回收的算法与实现》的学习笔记，目标是能够描述清楚各种 GC 算法的复杂度、优缺点。

基础概念 #

GC（Garbage Collection） #

即垃圾回收，是管理堆中已分配对象的机制。

对象（Object） #

对象在 GC 里的概念是：应用程序使用的数据的集合。对象可以分为头（header）和域（field）。头一般包含的信息有：对象的大小和对象的种类，一般情况下对象的使用者无法修改头信息；域中存的数据可能有两种类型：指针和非指针，指针指向内存空间某块区域的值，非指针就是值本身。

对象也分为活跃的对象和非活跃的对象，垃圾收集器只会回收确定不活跃的对象。

根（Root） #

根指的是所有对象的根对象，非常类似二叉树的根节点，程序中的对象都是从这个根对象开始向下分配。

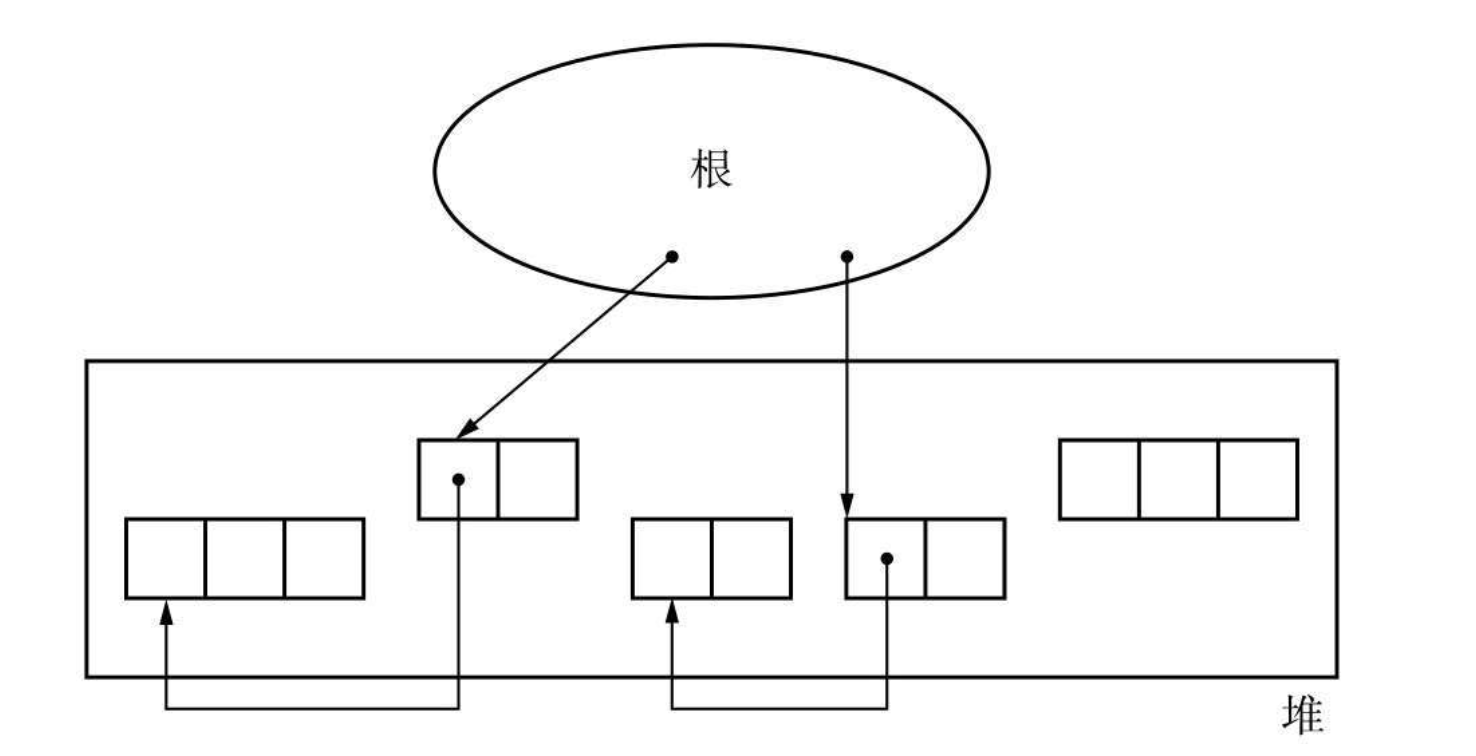
调用栈、寄存器以及全局变量空间都是根。

用户程序（Mutator） #

Mutator 是运行的用户程序，它实际进行的操作可以归为：生成对象和更新指针。

分配器（Allocator） #

Mutator 通过 Allocator（分配器）在内存上创建对象。对象的分配方法在不同回收算法中实现也有不同，因为这和垃圾回收逻辑的实现息息相关。

垃圾收集器（Collector） #

Collector 标记内存中的对象，并回收不需要的内存。

堆（Heap） #

堆是程序动态（一般就是指程序运行时）存放对象的空间，它在内存中由起始地址开始，一般是从低位地址向高位地址增长。堆的空间也是动态的，当没有足够的可用空间时就可以对堆进行扩容操作。

在初始状态下，堆被一个大的分块（chunk）所占据，然后，这个大的分块会被 Mutator 分割成合适的大小供活跃的对象使用，不久后对象转化为垃圾而被回收，被回收的空间再次成为分块，循环往复。

STW #

STW（Stop The World）是 GC 执行的过程中对应用程序产生的停顿。以早期的 Go 语言为例，为了执行垃圾回收，Go 会暂停用户协程的正常执行，转而执行垃圾回收，执行完毕后再恢复用户协程的执行，这期间就会造成应用程序的停顿。

很多有垃圾回收机制的语言实现的 GC 算法，大多会有 STW，比如 Java、Go。

评价标准 #

吞吐量：指 GC 单位时间内对象的处理量。

最大暂停时间：指的是 STW 占用的时间，时间越长，GC 性能也就越差。

堆使用率：体现在两个方面：

1. 对象头的大小：理论上头里的信息越多，GC 的决策效率也就越高，但是实际从空间角度看头还是越小越好。
2. 堆的用法：不同的 GC 算法有不同的堆空间的分配策略，下面可以详细看。

访问的局部性：由于寄存器和高速缓存、内存之间的处理速度、容量的差异，那从内存读取哪些数据到缓存也是一个可参考的点。一般来说，在堆中倾向把有引用关系的对象放在较近的位置，这样更容易一次性读取到。

常见算法 #

GC 标记 - 清除算法 #

标记清除算法分为两个阶段：标记和清除。

标记阶段（mark） #

标记阶段是把所有活动对象都做上标记的阶段，它从根对象开始遍历所有被根直接引用的对象，遍历的算法一般是深度优先搜索算法（DFS），因为 DFS 比 BFS 更能压低内存占用，此外还有广度优先搜索算法（BFS）。

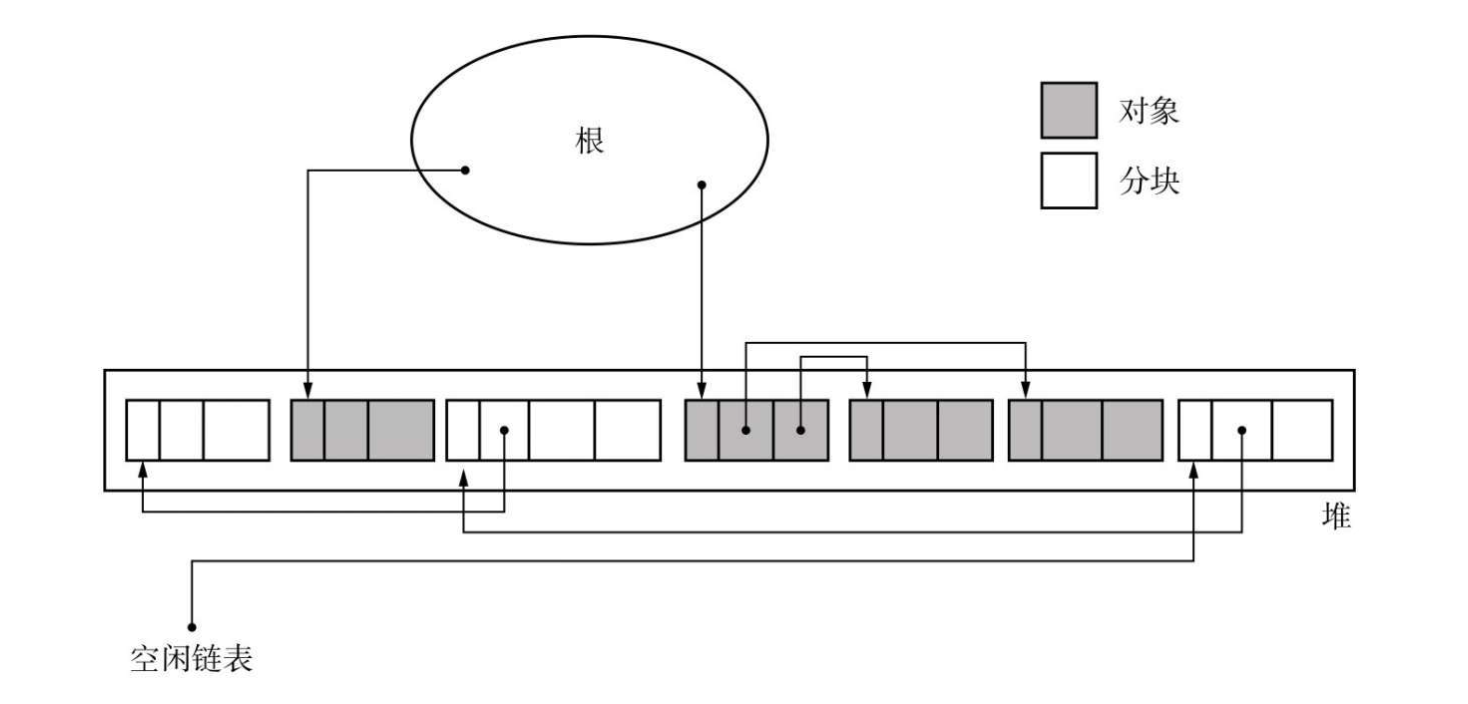
清除阶段（sweep） #

在清除阶段中，Collector 会遍历整个堆，回收没有打上标记的对象（即垃圾），被回收的垃圾会被连接到一个空闲链表等待进行再次分配，实际算法应用当中也可能会有多个这样的空闲链表。

为了减少清除算法所花费的时长，还可以通过延迟清除来减少 STW 的时间。

分配策略 #

Mutator 生成的对象都是大小不一的，那在空闲链表中，需要一定的算法才能将链表里的垃圾再利用，这种搜索链表并寻找大小合适分块的操作，就叫做分配。

一般分配策略有：First-fit、Best-fit 和 Worst-fit，一般推荐 First-fir，不推荐 Worst-fit 方法。

• 首次适应（First-Fit）：将链表里第一个大于新对象 size 的分块取出。

• 最优适应（Best-Fit）：会遍历链表，返回大于新对象 size 的最小分块。

• 最坏适应（Worst-Fit）：找出空闲链表中最大的分块，将其分割成 Mutator 申请的大小的部分和剩余的部分。

• 隔离适应（Segregated-Fit）：将内存分割成多个链表，每个链表中的内存块大小相同，申请内存时先找到满足条件的链表，再从链表中选择合适的分块；

• 循环首次适应（Next-Fit）从上次遍历的结束位置开始遍历，选择第一个大小大于申请内存的分块；

合并操作 #

如何链表中的连续分块在内存空间上也是连续的，那么就可以把这些小分块合成一个大分块，这种操作就是合并（coalescing）。

算法优点 #

1. 实现简单，容易实现。
2. 可以看到，标记清除算法本身不会移动对象的值，这个特性与下面的保守式 GC 算法兼容。

算法缺点 #

1. 垃圾回收阶段会 STW。
2. 内存会逐渐碎片化。
3. 分配策略 存在性能瓶颈，不管是 First-fit 还是 Best-fit 都会遍历链表，最糟的情况就是遍历到链表最后。
4. 与写时复制¹不兼容，于是很多进阶算法的实现引入了位图标记。

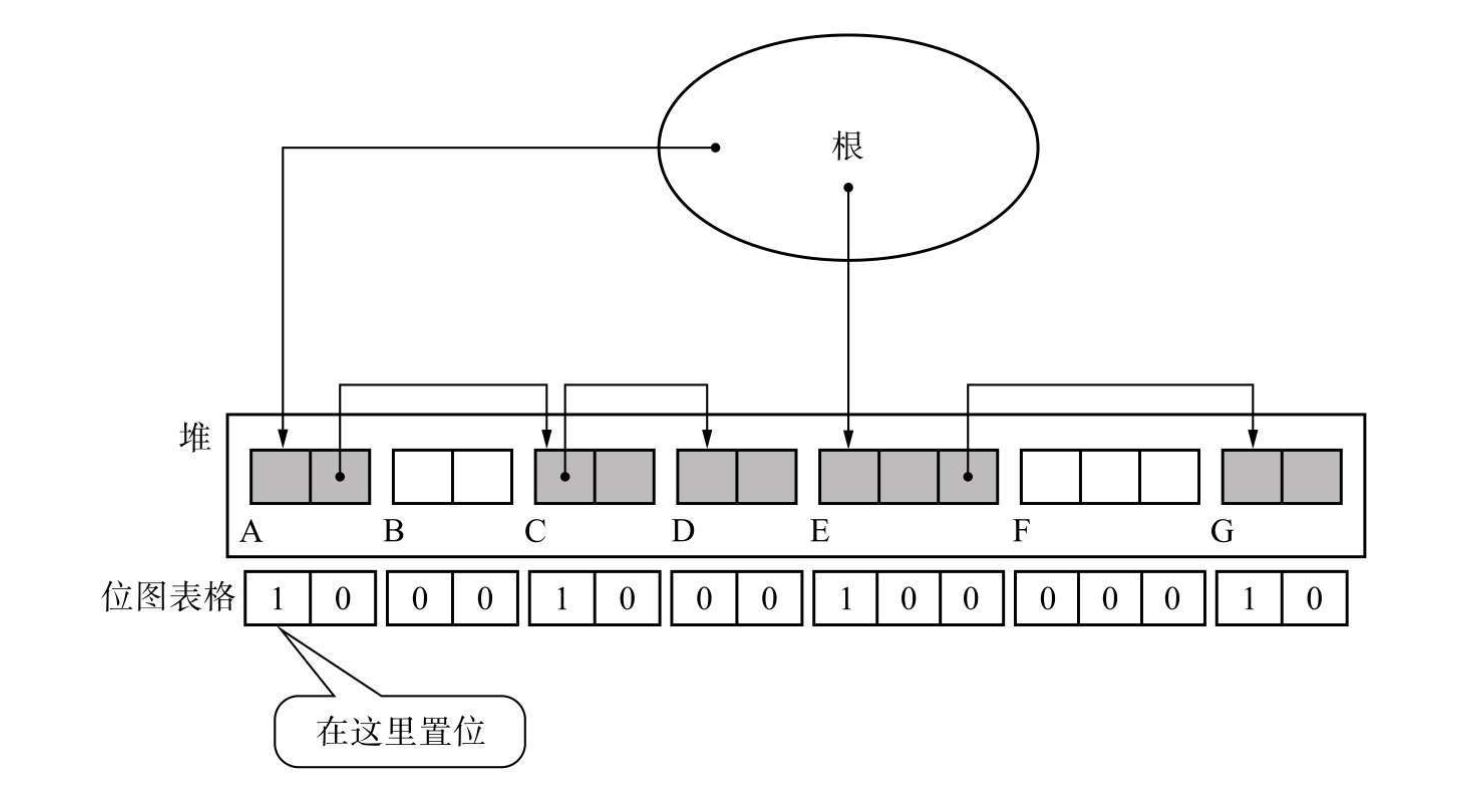
引用计数法 #

引用计数法（Reference Counting）和标记清除完全是另一种思路，它引入了一个“计数器”的概念，可以无需遍历，在进行引用的事先就记录下多少子对象引用自己，这个计数器一般内置在了对象头里面。于是在引用计数法中，就没有明确的垃圾清除阶段，当对象的引用计数为 0 时就可以被回收。

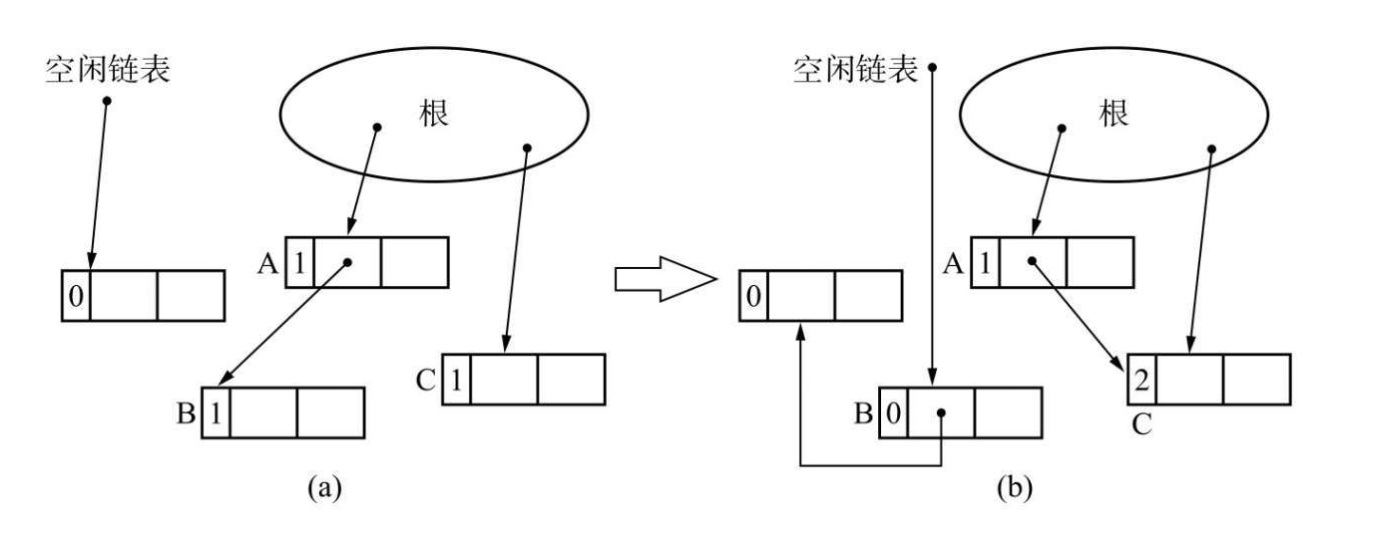
计数器的增减 #

在一个对象初始化的时候（从空闲链表取出一个分块），计数器默认的值就为 1，并返回其指针 ptr。当 ptr 指向的对象变成新的对象时，将旧对象的引用计数 -1 ，将新对象的引用计数 +1。

算法优点 #

1. 可以在引用为 0 时立刻回收垃圾，不需要从根遍历对象的引用关系（标记），减少了遍历的空间消耗和时间消耗（清除），这也意味着几乎没有 STW。

算法缺点 #

虽然看起来性能会非常好，但是它也有不少问题：

1. 会有垃圾之间循环引用的问题；
2. 计数器的增减处理操作会很多，一般会通过延迟引用计数来优化；
3. 存计数器的值需要占位，而且会很大。举个例子，如果是 32 位机器，那么空间大小约是 4G，即最多有 4G 的内存单位（对象）引用一个内存单位，即一个计数器的标志位必须要有 32 位的空间大小。
4. 理论上算法简单，根据各种语言语法（或语法糖）的实现，最终实现也会比较复杂，容易漏掉计数逻辑。

算法优化：着色 #

看到上面的缺点，应该能感觉到引用计数法的性能和空间问题还是挺严重的，但是“引用计数”相对于“标记-清除”的思路非常好，可以继续深入研究，于是又引出了“1 位引用计数法”和“着色标记-清除算法”。

具语言专家们观察，“几乎没有对象是被共用的，所有对象都能马上被回收”，所以上面提到的 32 位计数占位，可能可以优化掉。即用 0 表示引用计数为 1，用 1 表示引用计数大于 2 ，也可以有效地进行内存管理，但是需要处理好引用计数大于 2 时的归零问题。

另一方面，借鉴计数的标志位思路，也可以用“着色”的方式，对对象进行分类，通常如果分四类也只就需要 2 位的内存：

• 黑色：绝对不是垃圾的对象（初始化时）；
• 白色：绝对是垃圾的对象；
• 灰色：遍历搜索完毕的对象；
• 阴影：可能是循环垃圾的对象。

RC Immix 算法 #

2013 年出现的 RC Immix 算法是基于合并型引用计数法进行的改善，将 GC 的吞吐量低改善到了实用级别。

GC 复制算法 #

GC 复制算法的机制简单说就是只把某个空间里的活动对象复制到其他空间，把原空间里的所有对象都回收掉。在此，我们把复制活动对象的原空间成为 From 空间，将粘贴活动对象的新空间叫 To 空间。

GC 复制算法是利用 From 空间进行分配的。当 From 空间被完全占满时，GC 会将活动对象全部复制到 To 空间。当复制完成后，该算法会把 From 空间和 To 空间互换，GC 也就结束了。From 空间和 To 空间大小必须一致，这是为了保证能把 From 空间中的所有活动对象都收纳到 To 空间里。

在 GC 结束时，原空间的对象会作为垃圾被回收。因此，由根指向原空间对象的指针也会被重写成指向 To 空间新对象的指针。

复制机制 #

复制时，从根对象开始根据子对象的引用关系来遍历关系树，所有有关联的都是活跃对象了，一边遍历一边就可以复制到 To 空间，并对复制完的打上标记以进行并发控制即可。

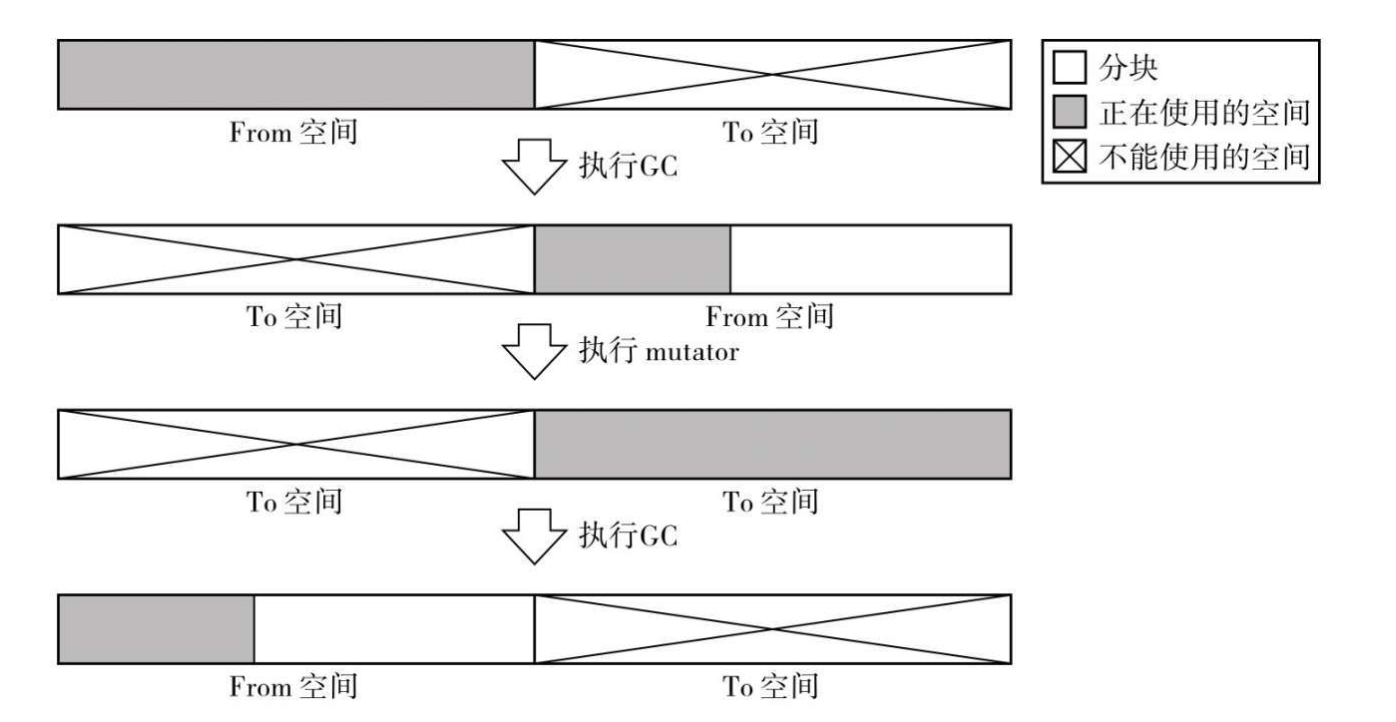
遍历完一次后，剩下的就是非活跃对象了，全部可以被直接回收，只要再交换一下 From 和 To 空间，GC 过程就结束了。

算法优点 #

1. 创建对象时不需要空闲链表中取，直接从 From 空间的剩余空间里分割出来，不需要遍历链表的分配策略。
2. 内存空间不会碎片化，这对内存管理是更加简单高效的，附带的实现问题也会更少。
3. 与“标记-清除”的步骤相比，复制操作只需要复制活动对象，虽然也会有 STW，但是操作简单粗暴而且有效，没有“标记”，也没有“清除”。
4. 复制后的对象一定程度上利用对象间的引用关系重新优化排布了空间位置，这对 CPU 读入高速缓存来说是件好事，因为附近关联的数据一次就被读入的概率更高了。

算法缺点 #

1. 因为 From 和 To 的空间必须一致，所以同时只能使用一半的堆空间，空间利用率低下。
2. 复制移动了对象的位置，不兼容保守式 GC 算法。

GC 标记 - 压缩算法 #

GC 标记 - 压缩算法是“CG 标记 - 清除”和复制算法结合的产物。上面我们已经看到了 GC 复制算法的很多诱人的优点，但是空间利用率属实不高，而“标记 - 清除”是用算法的复杂度换来了空间利用率的最佳方案之一。那么综合下来，GC 标记 - 压缩算法，它有和“标记 - 清除”一样的标记阶段，同时又增加了一个“压缩阶段”，所以空间上肯定是不用牺牲半个堆的空间了。

这个“标记 - 压缩”思路有好几种算法实现，比如 Lisp2 、Two-Finger、表格算法、ImmixGC 等算法，不再详细介绍，感兴趣可以去看书。

算法优点 #

1. 用算法复杂度又换取了一些空间，自然空间利用率就高了。

算法缺点 #

1. 算法复杂带来的是程序的性能问题会差一些。

保守式 GC #

保守式 GC 指的是不能识别指针和非指针的 GC。不能识别是否为指针，就会将非指针当做指针，将里面的值指向的对象当做了活动对象，并对其标记。因此垃圾被错误得保留下来，这种保守的处理方式就是保守式 GC。

相对应的，还有准确式 GC。准确式 GC 可以准确地分辨出指针和非指针，但是需要语言层面的支持。有很多算法的实现方式可以解决保守式 GC 的指针问题，比如 MostlyCopyingGC、Hans-J. Boehm 的黑名单算法。

算法优点 #

1. 算法的实现会更简单。

算法缺点 #

1. 想要识别指针还是非指针需要付出成本。
2. 垃圾会被保留下来占用堆空间，而且可能会持续增长。
3. 与很多算法不兼容，能够使用的算法有限。

分代垃圾回收 #

分代回收基于的一个假设是：大部分的对象在生成后马上就变成了垃圾，很少有对象能活得很久。这听起来好像没什么毛病，和日常写程序时的认识差不多。

在这种算法中，会有两种 GC，一种是新生代 GC，一种是老年代 GC。新生代 GC 将存活了一定次数的新生代对象当作老年代对象来处理，新生代对象上升为老年代对象的情况称为晋升（promotion）。在处理频率上，新生代 GC 的处理频率也会比老年代 GC 的频率高，因为老年代对象已经很少有真正的垃圾了。

算法优点 #

1. 性能。

算法缺点 #

1. 老年代 GC 的执行会增加 STW 时间。
2. 算法复杂，涉及跟多的内存管理机制。

增量式垃圾回收 #

增量式垃圾回收（Incremental GC）是一种通过逐渐推进垃圾回收来控制 STW 的时间的方法。与增量式相反的是停止式 GC，早期 Go 语言的垃圾回收就是停止式 GC，慢慢进化成增量式 GC。

增量式回收也是基于“标记-清除”算法的一种优化思路，具体的实现有三色标记法。

三色标记法 #

因为 Go 语言的垃圾回收就是三色标记法，我会在 Go 语言的垃圾回收机制 里再详细说。

算法特点 #

增量式垃圾回收不是一口气运行 GC，而是和 Mutator 交替运行的，因此不会长时间妨碍到 Mutator 的运行。增量式垃圾回收适合那些比起提高吞吐量，更重视缩短最大暂停时间的应用程序。

参考 #

垃圾回收的算法与实现

https://draveness.me/system-design-memory-management/