打家劫舍基本都可以用动态规划来解决。
房屋偷盗 #
环形房屋偷盗 #
维护一个 helper,设定 number 的起始位置,自底向上计算两次,取最大值。
var rob = function(nums) {
if (nums.length === 0) {
return 0
}
if (nums.length === 1) {
return nums[0]
}
let result1 = helper(nums, 0, nums.length - 2)
let result2 = helper(nums, 1, nums.length - 1)
return Math.max(result1, result2)
};
var helper = function(nums, start, end) {
let left = nums[start]
let right = 0
if (start < end) {
right = Math.max(nums[start], nums[start+1])
}
for (let i = start+2; i <= end; i++) {
let temp = left
left = right
right = Math.max(temp + nums[i], right)
}
return Math.max(left, right)
}
打家劫舍 III #
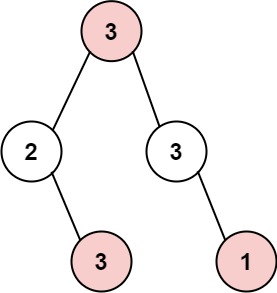
还是动态规划,但是数组变成了二叉树。
粉刷房子 #
分成三个公式,分别表示 r(i)、g(i)、b(i)。
然后还是滚动数组的思想,只构造一个三行两列的二维数组,保存 (i-1) 和当前 i 的最小花费,最后做一下比较。
var minCost = function(costs) {
let n = costs.length
if (n === 1) {
return Math.min(costs[0][0], costs[0][1], costs[0][2])
}
let dp = [[],[],[]]
for (let i = 0; i < 3; i++) {
dp[i] = [costs[0][i], 0]
}
for (let i = 1; i < n; i++){
for (let j = 0; j < 3; j++){
dp[j][i%2] = Math.min(dp[(j+2)%3][(i-1)%2], dp[(j+1)%3][(i-1)%2]) + costs[i][j]
}
}
let last = (n-1)%2
return Math.min(dp[0][last], dp[1][last], dp[2][last])
};