B 树是为磁盘或其他直接存取的辅助存储设备而设计的一种平衡搜索树。B 树类似于红黑树，但它们在降低磁盘 I/O 操作数方面要更好一点，比如很多数据库都使用 B 树或 B 树的变种来存储信息。

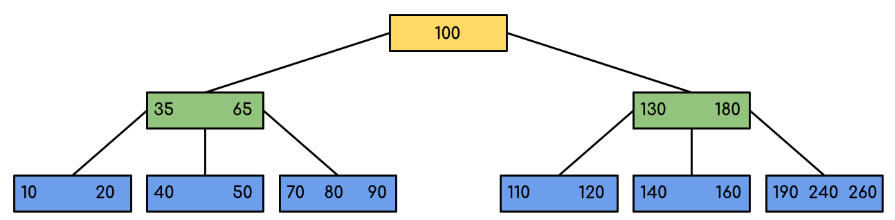
B 树 #

B 树有的地方也称 B-tree，但不要叫“B 减树”。B 树与红黑树的不同之处在于 B 树的结点可以有从数个到数千个很多孩子，也就是说，一个 B 树的“分支因子”可以相当大，它通常依赖于所使用的磁盘单元的特性。

由于在大部分系统中，一个 B 树算法的运行时间主要由它所执行的磁盘读和写的次数决定，所以我们希望这些操作能够读或写尽可能多的信息。因此，一个 B 树结点通常和一个完整磁盘页一样大，并且磁盘页的大小限制了一个 B 树结点可以含有的孩子个数。比如一棵分子因子为 1001、高度为 2 的 B 树，它可以存储超过 10 亿个关键字。由于根节点可以持久地保存在主存中，所以在这棵树中查找某个关键字至多只需要两次磁盘存取。

任何和关键字相联系的“卫星数据”将于关键字一样存放在同一个结点中，而且多数情况下，人们只是为每个关键字 key 存放一个指针，这个指针指向存放该关键字的卫星数据的磁盘页。

性质 #

除了上面简单介绍的之外，一棵 B 树 T 还具有以下性质的有根树（根为 T.root）：

1. 每个结点 x 有以下属性：
   1. x.n，当前存储在结点 x 中的关键字（非子结点概念）个数。
   2. x.n 个关键字本身 $x.key_1$、$x.key_2$、$x.key_3$ … $x.key_n$ 以非降序存放，使得 $x.key_1$ <= $x.key_2$ <= … <= $x.key_n$
   3. x.leaf ，一个布尔值，如果 x 是叶结点，则为 True；如果 x 为内部结点，则为 False
2. 每个内部结点 x 还包含 x.n+1 个指向其孩子的指针 x.c1、x.c2、x.c3、$x.c_{x.n+1}$ ，叶子结点没有孩子，所以它们的 $c_i$ 属性没有定义。
3. 关键字 $x.key_i$ 对存储在各子树中的关键字范围加以分割：如果 $k_i$ 为任意一个存储在以 $x.c_i$ 为根的子树中的关键字，那么 $k_1$ <= $x.key_1$ <= $k_2$ <= $x.key_2$ <= … <= $x.key_{x.n}$ <= $k_{x.n+1}$ 。
4. 每个叶结点具有相同的深度，即树的高度 h
5. 每个结点所包含的关键字个数有上界和下界，用一个被称为 B 树的最小度数的固定整数 t>=2 来表示这些界。
   1. 除了根结点以外的每个结点必须至少有 t-1 个关键字，因此，除了根结点以外的每个内部结点至少有 t 个孩子，如果树非空，根结点至少有一个关键字。
   2. 每个结点至多可包含 2t-1 个关键字，因此，一个内部结点至多可有 2t 个孩子，当一个结点恰好有 2t-1 个关键字时，称该结点是满的（full）。

虽然和红黑树一样，B 树每棵包含有 n 个结点的 B 树的高度为 $O(lgn)$。但是 B 树的分支可以非常大，故 log 计算的底数就非常大。严格来说，如果 n >= 1，那么对于任意一棵包含 n 个关键字、高度为 h、最小度数 t >= 2 的 B 树 T，有：

$$ h <= log_t{\frac{n+1}{2}} $$

基本操作 #

搜索 #

初始化 #

插入 #

在二叉搜索树中，要先查找插入新关键字的叶结点的位置。然而在 B 树中，不能简单地创建一个新的叶结点，然后将其插入，因为这样得到的树将不再是合法的 B 树，相反，我们是将新的关键字插入一个已经存在的叶结点上。

由于不能将关键字插入一个满的叶结点，此时需要引入一个操作，讲一个满的结点 y 按其中间关键字 $y.key_t$ 分裂成两个各含 t-1 个关键字的结点。中间关键字被提升为 y 的父结点，以标识两个新树的划分点。但如果 y 的父结点也是满的，就必须在插入新的关键字之前将其分裂，最终满结点的分裂会沿着树向上传播。

分裂 #

接着分裂说，我们并不是要等到找出插入过程中实际要分裂的满结点时才做分裂。相反，当沿着树往下查找新的关键字所属位置时，就分裂沿途遇到的每个满结点。这样的话，每当要分裂一个满结点 y 时，就能确保它的父结点不是满的。

删除 #

从 B 树删除关键字与插入操作类似，但是是反方向的，略微复杂一点。

B+ 树 #

B+ 树是 B 树的一个变种，它把所有的卫星数据都存储在叶结点中，内部结点只存放关键字和孩子指针，因此最大化了内部结点的分支因子。

B* 树 #

R 树 #

R* 树 #

参考 #

算法导论第 18 章