红黑树也是一种自平衡二叉搜索树,但不同的是,红黑树在每一个结点上增加了一个存储位来表示结点的颜色,可以是 Red 或 Black,通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出 2 倍,因而是近似于平衡的。红黑树的应用非常广,比如 epoll,研究相关底层原理时最好提前了解一下。
属性 #
红黑树中的每个结点包含 5 个属性:
color颜色,Red or Blackkey平衡二叉树中用于比较的值left左子结点right右子结点pparent,父亲结点
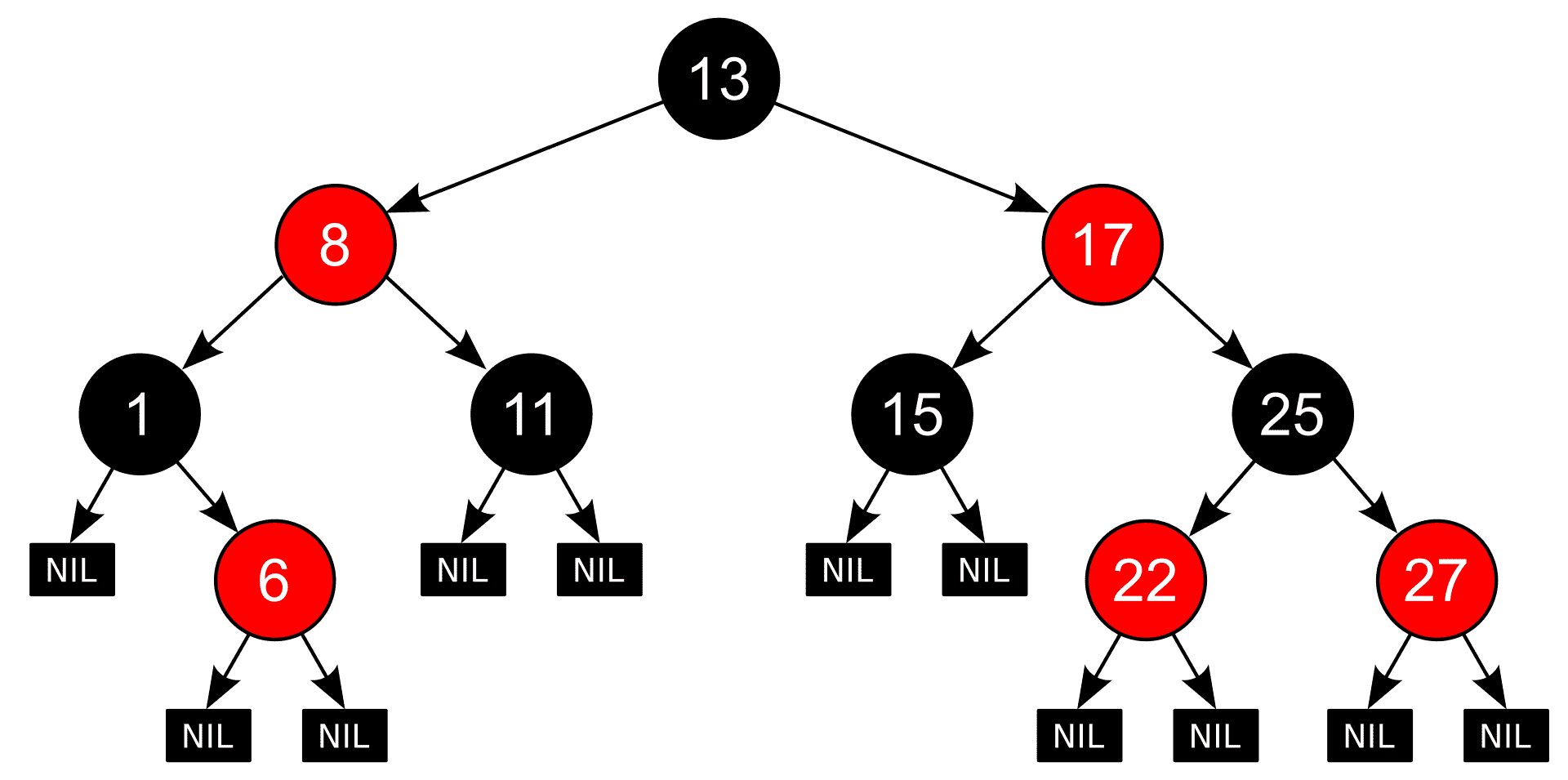
性质 #
红黑树也是一棵二叉搜索树,这意味着红黑树有二叉搜索树的性质:
- 左子树的所有节点值小于根的节点值(注意不含等号)
- 右子树的所有节点值大于根的节点值(注意不含等号)
- 没有键值相等的节点
同时一棵红黑树也是满足下面红黑性质的二叉搜索树:
- 每个结点或是红色的,或是黑色的。
- 根结点是黑色的。
- 每个叶结点(nil)是黑色的。
- 如果一个结点是红色的,则它的两个子结点都是黑色的。
- 对每个结点,从该结点下降到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。
这些约束确保了红黑树的关键特性:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
高度 #
从某个节点 x 出发(不包含 x )到达一个叶结点的任意一条简单路径上的黑色结点个数称为该结点的黑高,于是定义红黑树的黑高为其根结点的黑高,根的黑高至少为 $h/2$,于是 n 个结点的红黑树有:
$$n \geqslant 2^{h/2}-1 $$
转化一下,可得一棵有 n 个内部结点的红黑树的高度至多为:
$$2 lg(n+1)$$
操作 #
旋转 #
通过旋转,可以保持红黑树在插入和删除结点后仍能保持红黑树是一棵二叉搜索树的性质。不管是左旋还是右旋都可在 $O(1)$ 的时间内运行完成,在旋转操作中只有指针改变,其他所有属性都保持不变。
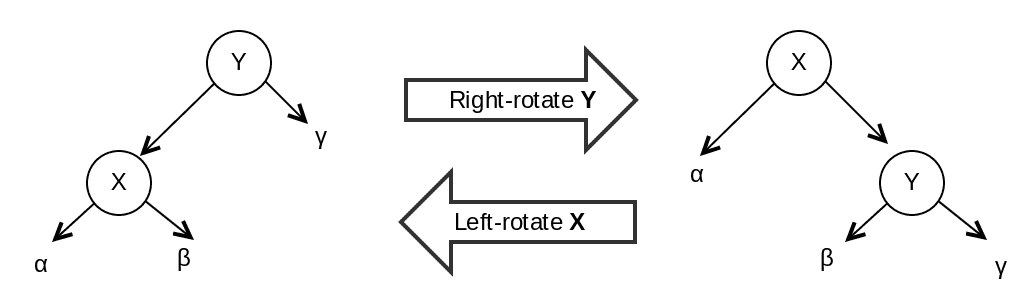
左旋 #
以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。
右旋 #
以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。
着色 #
红黑树通过旋转和变色达到自平衡状态,变色的原则分为多种情况,这个过程需要在一个 while 循环中保持三个不变式:
- 结点
z是红结点。 - 如果
z.p是根节点,则z.p是黑结点。 - 如果有任何红黑性质的破坏,则至多只有一条被破坏,或是性质 2,或是性质 4
着色的目的是为了达到近似平衡,一些资料里会通过把红色结点画平来理解,参考《算法4》3.3 节。
插入 #
我们可以在 $O(n)$ 的时间内完成向一棵含 n 个结点的红黑树中插入一个新结点 z。插入首先需要解决的是插入位置,这个过程和二叉查找树的逻辑一致,只要满足二叉查找树的性质即可,并且先将其标为红色。
如果一开始设为黑色,就会导致根到叶子的路径上有一条路上,多一个额外的黑节点,这个是很难调整的。但是设为红色节点后,可能会导致出现两个连续红色节点的冲突,那么可以通过颜色调换(color flips)和树旋转来调整。
此时需要通过着色和旋转达到自平衡状态,最多需要两次旋转就可以达到自平衡。
删除 #
与 n 个结点的红黑树上的其他基本操作一样,删除一个结点要花费 $O(lgn)$ 时间,与插入操作相比,删除操作要稍微复杂些,但删除操作最多需要三次旋转就可以达到自平衡。
与 AVL 树的区别 #
首先两者插入、查找的时间复杂度都是 $O(logN)$ ,但是红黑树只是大致平衡,而 AVL 树左右两个子树的高度差的绝对值不超过 1 。另外红黑树在颜色的加持下可以保证最多只需要三次旋转就能达到平衡,而 AVL 不能预知旋转次数,故红黑树的插入和删除更加稳定。
红黑树的扩张 #
顺序统计树 #
在红黑树基础上,还扩张除了顺序统计树(order-statistic tree)的数据结构,支持快速顺序统计操作。除了红黑树的结点外,还包括一个属性 size,这个属性包含了以当前 x 为根的子树的结点数,即这棵子树的大小。有等式:
$$ x.size = x.left.size + x.right.size + 1 $$
区间树 #
区间树是一种对动态集合进行维护的红黑树,其中每个元素 x 都包含一个区间 x.int。
参考 #
算法导论 12、13、14 章