基本概念 #
父节点,子节点,叶子节点 #
叶子节点: 一棵树当中没有子结点的结点称为叶子结点。
高度和深度 #
- 树的高度:节点到叶子节点的最大值就是其高度。
- 树的深度:高度和深度是相反的,高度是从下往上数,深度是从上往下。
注意: 一般默认是把根节点的深度设为 1,把子节点的高度设为 1,比如 104. 二叉树的最大深度。在面试的时候最好要确认一下。
var maxDepth = function(root) {
if (!root) return 0
return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
};
一些特性 #
- 在二叉树的第 i 层上至多有 $ 2 ^ { i-1 } $ 个结点(i>=1)
- 深度为 k 的二叉树最多有 $ 2^{k}-1 $ 个结点(k>=1)。
- 如果树有 n 个节点,则有 n-1 条边
- 如果有 a 个叶节点,则有 a-1 个非叶节点
- 具有 n 个节点的树最小深度为 $log_2n+1$
JavaScript #
function TreeNode(val, left, right) {
this.val = (val===undefined ? 0 : val)
this.left = (left===undefined ? null : left)
this.right = (right===undefined ? null : right)
}
Golang #
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}
数据结构 #
满二叉树 #
对于满二叉树,除最后一层无任何子节点外,每一层上的所有结点都有两个子结点二叉树。
完全二叉树 #
定义1:若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
定义2:对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
对称二叉树 #
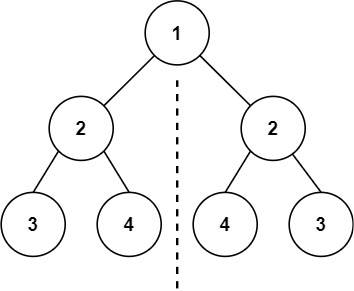
二叉搜索树 #
特点:
- 左子树的所有节点值小于根的节点值(注意不含等号)
- 右子树的所有节点值大于根的节点值(注意不含等号)
- 没有键值相等的节点
由此可得:
二叉搜索树的中序遍历结果是一个有序列表,这个性质很有用。
但是二叉搜索树不一定平衡,因此引申出平衡二叉搜索树。
平衡二叉查找树可以修复二叉查找树形状不规则的问题。
平衡二叉树(AVL 树) #
平衡二叉树(Adelson-Velsky and Landis Tree)具有二叉搜索树的性质,同时又多了以下特性:
- 除了空树,任何一个结点的左子树与右子树都是平衡二叉树,并且高度之差的绝对值不超过 1。
- 平衡二叉树在插入新的子节点时,可能会形成最小失衡子树。
- 平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式,左旋 与 右旋 。
二叉树遍历 #
深度优先搜索(DFS) #
先、中、后指的是根节点的先后。
递归方式按照这个模板推导即可。
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 前序位置
traverse(root.left);
// 中序位置
traverse(root.right);
// 后序位置
}
先序遍历 #
非递归实现
var preorderTraversal = function(root) {
let stack = []
let ret = []
while (root || stack.length) {
while (root) {
ret.push(root.val)
stack.push(root)
root = root.left
}
root = stack.pop()
root = root.right
}
return ret
};
中序遍历 #
非递归实现
var inorderTraversal = function(root) {
const res = [];
const stk = [];
while (root || stk.length) {
while (root) {
stk.push(root);
root = root.left;
}
root = stk.pop();
res.push(root.val);
root = root.right;
}
return res;
};
后序遍历 #
后序的遍历顺序会相对比较有用,在后序位置时 root 节点已经遍历过其子树信息,可以进行一系列的判断。
反向构建 #
广度优先搜索(BFS) #
同层序遍历。
层次遍历 #
BFS 迭代方案 #
var levelOrder = function(root) {
let ret = []
if (!root) {
return ret
}
let q = []
q.push(root)
while (q.length) {
let level = q.length
ret.push([])
for (let i = 1; i <= level; i++) {
let node = q.shift()
ret[ret.length - 1].push(node.val)
if (node.left) q.push(node.left)
if (node.right) q.push(node.right)
}
}
return ret
};
这里利用队列的方式进行遍历子节点,循环进行先入先出。
DFS 递归方案 #
DFS 递归方案比较常规,需要一个全局的数组和一个表示层级的 level 索引:
var levelOrder = function(root) {
let ret = []
let helper = function(root, level) {
if (!root) return
if (ret.length === level) ret.push([])
ret[level].push(root.val) // 这里是先序,改成中序、后序都可以。
helper(root.left, level + 1)
helper(root.right, level + 1)
}
helper(root, 0)
return ret
};
常见操作 #
翻转二叉树 #
226. 翻转二叉树 考虑递归实现。
var invertTree = function(root) {
if (!root) {
return root
}
let left = invertTree(root.left)
let right = invertTree(root.right)
root.left = right
root.right = left
return root
};
其他题型 #
公共祖先问题(LCA) #
解决 LCA 问题的核心是理解:如果一个节点能够在它的左右子树中分别找到 p 和 q,则该节点为 LCA 节点。
var lowestCommonAncestor = function (root, p, q) {
let find = function (root, p, q) {
if (root === null) return null;
if (root === p || root === q) return root;
let left = find(root.left, p, q);
let right = find(root.right, p, q);
if (left !== null && right !== null) return root;
return left !== null ? left : right;
};
find(root, p, q);
};
todo #
589. N 叉树的前序遍历(熟悉 N 叉树)
662. 二叉树最大宽度 (请分别使用 BFS 和 DFS 解决,空间复杂度尽可能低)
967. 连续差相同的数字 (隐形树的遍历)
1145. 二叉树着色游戏(树上进行决策)