本节目的只是了解基本的微积分概念，太高级的还是回去看《高等数学》上下两册吧。

参考 #

基础概念也可以直接上数学乐，非常易懂。

极限 #

以函数 $f(x) = \frac{1}{x}$ 为例，我们可以探讨当 $x$ 趋近于无穷大 $(x \to \infty)$ 或趋近于零 $(x \to 0)$ 时，$f(x)$ 的极限行为。

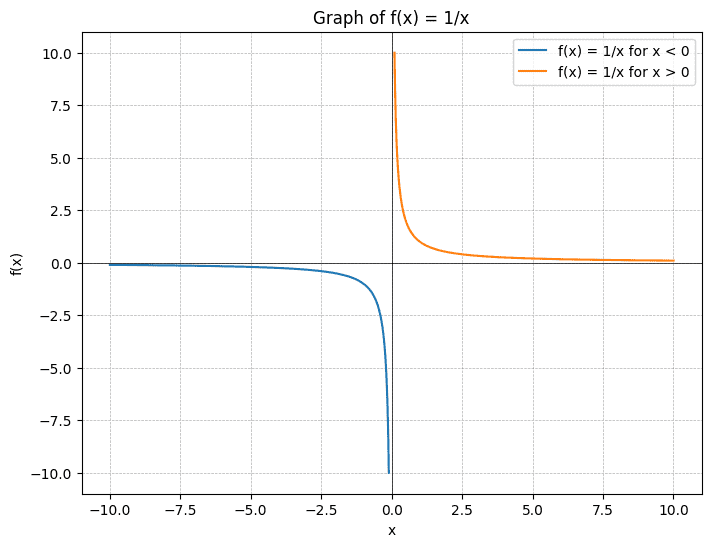
当 $x$ 趋近于无穷大

当 $x$ 的值变得非常大时，$\frac{1}{x}$ 将会变得非常小，趋近于 0。数学上，我们可以表示为：

$\lim_{x \to \infty} \frac{1}{x} = 0$

这意味着，随着 $x$ 值的增加，$\frac{1}{x}$ 的值会无限接近于 0，但永远不会等于 0。

当 $x$ 趋近于 0

从正方向趋近于 0 $(x \to 0^+)$ ：当 $x$ 的值从正数方向无限接近于 0 时，$\frac{1}{x}$ 的值将会变得非常大，趋近于正无穷。数学上，我们可以表示为：

$\lim_{x \to 0^+} \frac{1}{x} = +\infty$

从负方向趋近于 0 $(x \to 0^-)$ ：当 $x$ 的值从负数方向无限接近于 0 时，$\frac{1}{x}$ 的值将会变得非常小，趋近于负无穷。数学上，我们可以表示为：

$\lim_{x \to 0^-} \frac{1}{x} = -\infty$

这两种情况说明，当 $x$ 从不同的方向趋近于 0 时，$\frac{1}{x}$ 的极限行为是不同的。从正方向接近 0 时，它的极限是正无穷；从负方向接近 0 时，它的极限是负无穷。

导数（Derivative） #

推导 #

设有函数 $f(x)$，则它在某一点 $x$ 处的导数 $f’(x)$ 可以表示为：

$f’(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$

在这个公式中，$\Delta x$ 表示自变量 $x$ 的变化量。这个公式实际上就是导数的定义，表示函数 $f(x)$ 在点 $x$ 处的变化率。当 $\Delta x$ 趋向于零时，我们得到了函数在该点的切线的斜率，即导数。导数是指一个函数在某一点处的变化率，描述了函数在给定点的切线的斜率，即函数在该点的局部变化率。导数通常表示为 $f’(x)$ 或 $\frac{df}{dx}$，表示函数 $f(x)$ 对自变量 $x$ 的变化率。

以 dy/dx 来看导数 #

当我们考虑一个函数 $y = f(x)$ 在某一点 $x$ 处的导数时，我们实际上在寻找这个函数在该点的切线的斜率，也就是说，我们在找出这个函数在该点的局部变化率。假设我们想要计算点 $x$ 处的导数，我们引入一个很小的变化量 $\Delta x$。现在，我们有两个点，一个是 $x$，另一个是 $x + \Delta x$。在这两个点上，函数的值分别是 $f(x)$ 和 $f(x + \Delta x)$。

函数值的变化量为 $\Delta y = f(x + \Delta x) - f(x)$，而自变量的变化量为 $\Delta x$。导数的定义告诉我们，导数可以通过这个变化量的比率来计算。因此，我们将 $\Delta y$ 除以 $\Delta x$，得到的就是函数在点 $x$ 处的平均变化率。

$\text{平均变化率} = \frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) - f(x)}{\Delta x}$

现在，为了获得函数在点 $x$ 处的确切变化率，我们需要让 $\Delta x$ 趋向于零。这个过程被表示为一个极限：

$\text{导数} = \frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}$

而这个极限就是导数的定义，它告诉我们函数在点 $x$ 处的变化率，即函数在该点的切线的斜率。

二次导数 #

二次导数，也称为二阶导数，是指一个函数的导数的导数。它表示了函数变化率的变化率，或者说函数的曲率。更具体地说，二次导数告诉我们原函数的斜率如何随着自变量的变化而变化。

考虑一个函数 $y = f(x)$，它的一阶导数 $f’(x)$ 表示了函数 $f(x)$ 的斜率随着 $x$ 的变化而变化的情况。二次导数 $f’’(x)$ 则表示了这个斜率的变化率，也就是说，它表示了函数曲线的曲率或弯曲程度。

二次导数的正负号可以告诉我们函数曲线是凹向上还是凹向下。如果二次导数为正，表示函数曲线在该点处凹向上，意味着函数的斜率在这个点附近是增加的，函数的曲线呈现向上的弯曲。如果二次导数为负，表示函数曲线在该点处凹向下，意味着函数的斜率在这个点附近是减少的，函数的曲线呈现向下的弯曲。

总之，二次导数提供了关于函数曲线的更多信息，特别是关于其曲率的信息，这对于分析函数的局部特性和函数图像的形状非常有用。

导数法则 #

公式列表可参考

• https://shuxuele.com/calculus/derivatives-rules.html
• https://en.wikipedia.org/wiki/Differentiation_rules

求极值 #

导数可以用来求极值，高数必考题。

微分（Differential） #

微分描述了当一个量（通常是自变量）发生极小变化时，另一个量（通常是函数值）的变化情况。微分可以提供函数在特定点附近的局部变化率信息，这对于理解和预测各种现象非常有用。

微分的直观理解 #

假设有一个函数 $f(x)$，它描述了某个变量 $x$ 和另一个变量 $y$ 的关系，即 $y = f(x)$。当 $x$ 发生一个非常小的增加 $dx$ 时，$y$ 相应的变化量 $dy$ 称为 $f(x)$ 在 $x$ 点的微分，记作 $df$ 或 $dy$。这个变化量 $dy$ 可以通过函数的导数 $f’(x)$ 与 $dx$ 的乘积来近似，即：

$dy = df = f’(x) \cdot dx$

微分的数学定义 #

从数学的角度来看，微分是基于导数的概念定义的。如果一个函数 $f(x)$ 在点 $x$ 处可导，那么函数在 $x$ 处的微分 $df$ 定义为：

$df = f’(x) \cdot dx$

其中，$f’(x)$ 是函数在 $x$ 点的导数，$dx$ 是自变量 $x$ 的一个无穷小增量，$df$ 是因 $x$ 的增量 $dx$ 而引起的函数值 $f(x)$ 的近似增量。

微分的应用 #

微分在数学、物理、工程学和经济学等多个领域都有广泛的应用。它不仅用于计算变化率（如速度是位置的微分，加速度是速度的微分），还用于求解最值问题、优化问题、预测模型的局部行为，以及在微分方程中描述复杂系统的动态变化等。

导数和微分的区别 #

导数主要描述的是函数在某一点处的瞬时变化率或斜率。具体来说，如果有一个函数 $f(x)$，它在点 $x$ 的导数 $f’(x)$ 表示的是，当 $x$ 发生一个极小的变化时，$f(x)$ 相对于 $x$ 的变化率。数学上，导数定义为：

$f’(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}$

这个定义表明，导数是一个极限过程的结果，反映了函数在某一点附近的局部线性行为。

微分则更多地关注于函数值的实际变化量。当我们说函数 $f(x)$ 在点 $x$ 的微分时，我们指的是在 $x$ 发生一个小变化 $dx$ 时，$f(x)$ 的变化量 $df$。如果函数在 $x$ 处可导，则这个变化量可以用导数来近似：

$df = f’(x) \cdot dx$

这里，$dx$ 是自变量的一个小变化，$df$ 或 $dy$ 是函数值的相应变化，而 $f’(x)$ 是函数在 $x$ 点的导数。

• 本质上，导数是一个比率，描述了函数在某点的瞬时变化率；而微分是一个实际的变化量，描述了当自变量变化一个小量时，函数值的近似变化量。
• 表达方式，导数通常表示为 $f’(x)$ 或 $\frac{dy}{dx}$，强调变化率；微分则表示为 $dy$ 或 $df$，强调实际变化量。
• 应用角度，导数用于解析函数的局部性质，如判断函数的增减、求极值等；微分则更多地用于实际问题中近似计算小的变化，以及在微分方程、积分计算中发挥作用。

尽管导数和微分是两个不同的概念，但它们是密切相关的，导数是微分的基础，而微分则是导数的应用展现。

积分 #

积分是微积分的另一个重要概念，与微分相反，它表示函数在一段区间上的累积效应或总量。在符号上，如果我们用 $\int$ 来表示积分，那么函数 $f(x)$ 在区间 $[a, b]$ 上的积分可以表示为：

$\int_{a}^{b} f(x) , dx$

这个符号表示了在区间 $[a, b]$ 上函数 $f(x)$ 的面积。其中 $dx$ 表示自变量 $x$ 的变化量，而 $\int_{a}^{b}$ 则表示我们对 $x$ 从 $a$ 积累到 $b$ 的过程。积分主要分为两类：不定积分和定积分。

不定积分（Antiderivative） #

不定积分的本质是求导数的逆过程，主要关注函数的原函数。如果函数 $F(x)$ 的导数是 $f(x)$，即 $F’(x) = f(x)$，那么我们说 $F(x)$ 是 $f(x)$ 的一个原函数。不定积分的符号是 $\int f(x) , dx$，表示所有可能的原函数 $F(x)$ 加上一个常数 $C$（因为导数的过程会丢失一个常数信息）。即：

$\int f(x) , dx = F(x) + C$ 其中，$\int$ 是积分符号，$f(x)$ 是被积函数，$dx$ 表示积分是关于变量 $x$ 进行的，$F(x)$ 是 $f(x)$ 的一个原函数，$C$ 是积分常数，表示有无穷多个原函数。

定积分（Definite Integral） #

对于定积分来说，你可以将区间 $[a, b]$ 分割成无数个小区间，每个小区间对应的小矩形的面积近似为 $f(x) \cdot \Delta x$，将这些小矩形的面积累加起来，当小区间的宽度趋向于零时，这个累加的和就趋向于函数 $f(x)$ 在 $[a, b]$ 区间上下的准确面积，这个过程就是定积分。

定积分关注的是在一个特定区间 $[a, b]) 上函数 (f(x)$ 下的面积。定积分的符号是 $\int_a^b f(x) , dx$，表示从 $a$ 到 $b$ 的区间上 $f(x)$ 与 $x$ 轴之间形成的净面积。定积分的计算可以通过求函数 $f(x)$ 在区间 $[a, b]$ 上的一个原函数 $F(x)$，然后利用基本定理计算 $F(b) - F(a)$ 来完成。即：

$\int_a^b f(x) , dx = F(b) - F(a)$

积分的本质 #

在本质上，积分可以理解为求面积、体积或其他量的过程，或者说是累加无限多个无穷小量的过程。

积分法则 #

计算法则参考列表：

• https://shuxuele.com/calculus/integration-rules.html