介绍 #
动态规划(Dynamic Programming,简称DP)常常适用于有重叠子问题和最优子结构性质的问题,并且记录所有子问题的结果,因此动态规划方法所耗时间往往远少于朴素解法。
使用动态规划解决的问题有个明显的特点,一旦一个子问题的求解得到结果,以后的计算过程就不会修改它,这样的特点叫做无后效性,求解问题的过程形成了一张有向无环图。动态规划只解决每个子问题一次,具有天然剪枝的功能,从而减少计算量。
识别问题 #
解决动态规划问题需要若干步骤,但首先要解决的是:识别出问题是否适合用动态规划解决。
如果题目是求一个问题的最优解(通常是最大值或最小值),或者求问题的解的数目(或判断问题是否存在解),那么这个问题有可能适用动态规划。
如果题目要求列出所有的解,那么很有可能是回溯法解决。
状态转移方程 #
解决动态规划问题最难的地方在于推导出 $f(n)$ 的状态转移方程,即用一个等式表示其中某一步的最优解和前面若干步的最优解的关系。
主要有以下步骤:
- 如何定义 $f(n)$;
- 如何通过 $f(1)$, $f(2)$, … $f(n - 1)$ 推导出 $f(n)$,即状态转移方程;
- 最后要注意的就是边界问题、终止条件等代码细节。
解题方法 #
动态规划有自底向上和自顶向下两种解决问题的方式。自顶向下即记忆化递归,自底向上就是递推。
推导过程:如果一个楼梯有 n 级台阶(台阶从 0 开始计数,从第 0 级一直到第 n-1 级),由于一次可以爬 1 级或 2 级台阶,因此最终可以从第 n-2 级台阶或第 n-1 级台阶爬到楼梯的顶部,如果用 $f(i)$ 表示从楼梯的第 i 级台阶再往上爬的最小成本,那么 $f(n-1)$ 和 $f(n-2)$ 的最小值就是这个问题的最优解。
然后开始求第 i 级台阶往上爬的最小成本,可以得出 $f(i)$ 的状态转移方程,得出 f(i) = min(f(i-1), f(i-2)) + cost[i]。
自顶向下 - 递归 #
如果将大问题分解成若干小问题之后,小问题相互重叠,那么直接用递归的代码实现就会存在大量重复计算。小问题之间存在重叠的部分,这是可以运用动态规划求解问题的一个显著特点。
func minCostClimbingStairs(cost []int) int {
n := len(cost)
// 到达 n 的花费
return min(helper(cost, n-2), helper(cost, n-1))
}
func helper(cost []int, i int) int {
if i < 2 {
return cost[i]
}
// 从 i 级往上爬的最小成本
return min(helper(cost, i-2), helper(cost, i-1)) + cost[i]
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
这是根据状态转移方程得出的最直接的解法,这种解法的时间复杂度是 $O(2^n)$ ,下面开始进一步优化。
自顶向下 - 加缓存 #
递归最大的问题就是每一步都有重复计算,而且重复程度是呈指数增长的。
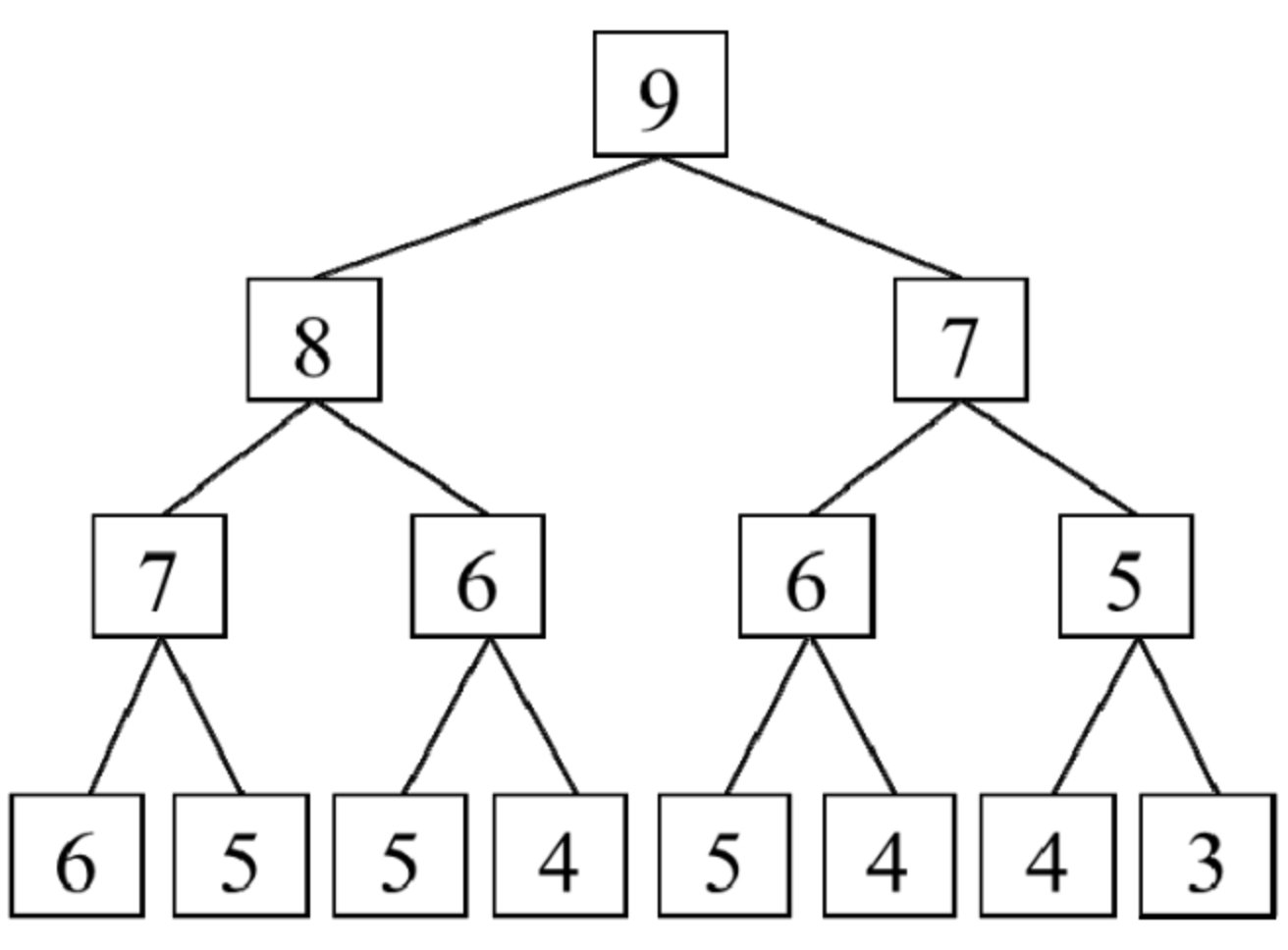
于是我们可以维护一个数组,将每个索引的结果都存储下来。
/**
* @param {number[]} cost
* @return {number}
*/
var minCostClimbingStairs = function(cost) {
if (cost.length === 0) {
return 0
}
let dp = []
let n = cost.length
helper(n, cost, dp)
return Math.min(dp[n-2], dp[n-1])
};
var helper = function(i, cost, dp) {
if (i < 2) {
dp[i] = cost[i]
return
}
helper(i - 1, cost, dp)
helper(i - 2, cost, dp)
dp[i] = Math.min(dp[i-1], dp[i - 2]) + cost[i]
}
这样只能降低一般的查询,同时需要维护一个长度为 n 的数组,所以时间和空间复杂度还是 $O(n)$ 。
自底向上 - 迭代 #
下面介绍与自顶向下相反的迭代方法:自底向上,也就是从 0 和 1 开始迭代。这种迭代的代码可以更好的控制计算的顺序,相对另外两种方法来说是更优解。
/**
* @param {number[]} cost
* @return {number}
*/
var minCostClimbingStairs = function(cost) {
if (cost.length === 0) {
return 0
}
let dp = [cost[0], cost[1]]
let n = cost.length
for (let i = 2; i < n; i ++) {
dp.push(Math.min(dp[i-1], dp[i-2])+cost[i])
}
return Math.min(dp[n-1], dp[n-2])
};
自底向上通常都需要维护一个长度为 n 的数组 dp,所以空间复杂度和时间复杂度都为 $O(n)$。
自底向上 - 优化空间 #
但是我们发现最终的结果其实一直只使用了 dp 的最后两位,就是说前面的内容是不需要的,可以根据这个性质,只维护一个长度为 2 的数组就可以了,从而将空间复杂度降到 $O(1)$。
var minCostClimbingStairs = function(cost) {
if (cost.length === 0) {
return 0
}
let dp = [cost[0], cost[1]]
let n = cost.length
for (let i = 2; i < n; i ++) {
dp[i%2] = Math.min(dp[0], dp[1])+cost[i]
}
return Math.min(dp[0], dp[1])
};
题目类型 #
单序列问题 #
单序列问题的输入通常是一个序列,比如一个数组或字符串。
解决单序列的问题的关键是根据题目的特点找出元素的最优解和前面若干(通常是一个或两个)元素的最优解的关系,进而推导出状态转移方程,最后只要避免重复计算,一般就可以解决。
解法也可以分为自顶向下和自底向上,注意自顶下先的递归方式一定要缓存数据避免重复计算。
自顶向下 #
TODO
自底向上 #
打家劫舍需要注意的另一个重要属性是,两个相邻的数不能相加,这点在代码里需要注意。
var rob = function (nums) {
n = nums.length;
if (n === 0) {
return 0;
}
let dp = [];
if (n > 0) {
dp.push(nums[0]);
}
if (n > 1) {
dp.push(Math.max(dp[0], nums[1]));
}
for (let i = 2; i < n; i++) {
dp.push(Math.max(dp[i - 2] + nums[i], dp[i - 1]));
}
return dp[n - 1];
};
上面还是维护了一个长度为 n 的数组,可以优化成下面的只基于两个元素的滚动数组(执行击败98%、内存击败93%)
var rob = function (nums) {
n = nums.length;
if (n === 0) {
return 0;
}
let first = 0
if (n > 0) {
first = nums[0];
}
let second = first
if (n > 1) {
second = Math.max(first, nums[1]);
}
for (let i = 2; i < n; i++) {
let temp = first
first = second
second = Math.max(temp + nums[i], second)
}
return second;
};
拆分成子问题 #
参考《剑指offer II》动态规划篇,维护两个公式。适合同样解法的还有 剑指 Offer II 091. 粉刷房子
其他例题 #
打家劫舍问题参考 经典问题 - 打家劫舍专题
双序列问题 #
双序列与单序列不同的是,输入一般是两个序列(字符串或数组),因此状态转移方程通常有两个参数,即 f(i, j),定义了第 $1$ 个序列中下标从 $0$ 到 $i$ 的子序列和第 $2$ 个序列中下标从 $0$ 到 $j$ 的子序列的最优解。一旦找到了 f(i, j) 与 f(i-1, j-1)、f(i-1, j) 和 f(i, j-1) 之间的关系,通常问题就可以解决。
矩阵路径问题 #
背包问题 #
一些例题 #
var maxSubArray = function(nums) {
if (nums.length === 0) {
return 0
}
let max = nums[0]
for (let i = 1; i < nums.length; i++) {
if (nums[i] < nums[i-1] + nums[i]) {
nums[i] += nums[i-1]
}
if (nums[i] > max) {
max = nums[i]
}
}
return max
};
var lengthOfLIS = function(nums) {
let dp = new Array(nums.length)
let ret = 0
for (let i = 0; i < nums.length; i ++) {
dp[i] = 1
for (let j = 0; j <= i; j++) {
if (nums[j] < nums[i]) {
dp[i] = Math.max(dp[i], dp[j] + 1)
}
}
ret = Math.max(ret, dp[i])
}
return ret
};
资料 #
https://leetcode.cn/leetbook/detail/dynamic-programming-1-plus/